Home About Links Blockfall rss

Logical Share Splitting

2023 Sep 10

Are mathematicians just not trying hard enough?

The Riemann hypothesis is one of the most important open problems in math. There's a $1 million prize from the Clay mathematics institute for a proof or disproof of the Riemann hypothesis. At the time of writing, it remains unsolved. From this, we may conclude that one cannot simply buy a solution to difficult mathematical problems.
Or could we? How do we know that buying a difficult maths proof is impossible? Perhaps the Clay mathematics institute is somehow not asking the question in the right way. And it's true that the value of a million dollars has been eroded over time by inflation. One might guess that a Riemann proof would be worth at least 100 million. Would that be enough to conjure it from the collective intelligence of humanity?
Simply directly declaring a $100 million reward for a solution would probably not work. For one thing, there's the issue of corollary-sniping where the prize wouldn't give anyone an incentive to publish solutions to hard intermediate steps of the problem, since the prize as a whole only goes to the one who solves the entire problem as a whole. For another, even the million dollar prize on its own would be plenty of reason for a money-motivated person to solve the problem if a solution were within their grasp. The issue is not merely one of funding, we humans are somehow failing to combine our efforts properly.

Prediction markets are pretty cool

One of the standard ways to buy knowledge is prediction markets. Can we try that here? John Wentworth describes here a scheme for using markets to get mathematical proofs. Here's a scheme that's very similar in the overall idea, though the exact rules are slightly different:
As Wentworth explains, the virtue of this system is that in order to redeem shares for a proposition you can prove, you need to reveal your proof to the people running the market. Not to other traders necessarily, but whatever the market mechanism is that is enabling the above rules, it can see the math proofs implied in the trades people make.

Logical share splitting

A common theme in mathematics is to split proofs up like this: First we show A ⇒ B, then we show A. This allows us to prove B. Part of the point of using a market is to combine the intelligence of the various traders in the market into something greater than any individual trader. So ideally, we'd like to be able to prove B, even if one trader can only prove A ⇒ B and the other trader can only prove A. So let's say there's some profit in proving B: Shares are trading at less than $1 (say $0.6), but we could redeem them for $1 if we could only prove B. Alice knows how to prove (redeem shares for) A. Bob knows how to prove (redeem shares for) A ⇒ B. How can they make money?
Logical share splitting provides a way. It works by permitting the exchange of a pair of shares for a different pair of shares in such a way that the possible payout of redeeming the shares remains unchanged. This is a new share exchange rule, it isn't possible to make an equivalent trade using any of the previously described rules. The rule:
The logic behind why payouts remain the same is as follows: Consider how many of the propositions A, B are true. The number is 0, 1, or 2. If neither is true, then the shares in each are worth nothing, and the combined shares are also worth nothing. If one is true and one is false, then the combined A∨B share is worth $1, while the combined A∧B share is worth nothing. Finally, if both are true, then each of the combined shares is worth $1.
the identity A + B = A∧B + A∨B expressed in terms of 2x2 tables
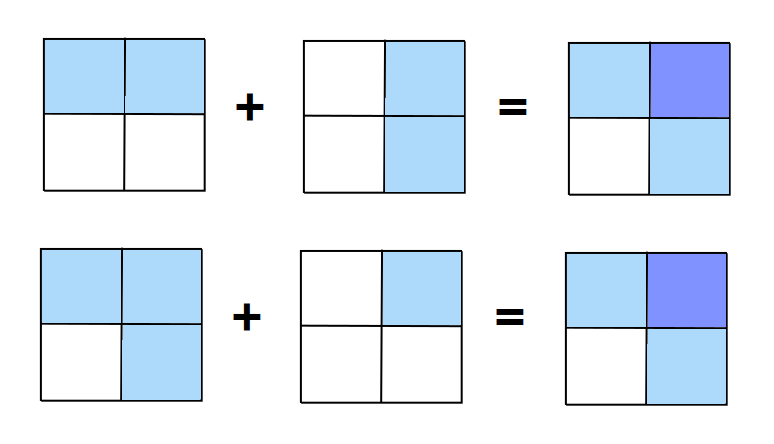
So now let's see how Alice and Bob can make money on shares in B by combining their proofs of A and A ⇒ B. First Alice, who can prove A, produces many many shares of ¬A for free. This is doable if you have a proof for A by starting from a bunch of free ⟂ shares and using equivalent exchange. She sells these for $0.2 each to Bob, pure profit. Then Bob purchases many many shares of B. These are not purchased from the market mechanism, which only sells ⊺ or ⟂ shares, but rather on the open market, which in this scenario prices them at $0.6. Given a share each of B and ¬A, logical share splitting then allows exchanging them for¬A∨B and ¬A∧B. The latter shares are worthless, since we know that A is true. But the former shares are equivalent to A ⇒ B and since Bob has a proof of this, they can be redeemed for $1. This gives a profit of $0.2 for Bob. Alice and Bob's combined profits come to $0.4, exactly the difference between the $0.6 price of shares in B and the $1 they should be worth, given that B has a proof.
(It's important to note that logical share splitting wasn't required to make this work. After all, Alice and Bob together had a proof of B so they could have just passed shares back and forth between them, conjoining their sub-theorems as required and removing them after they were no longer needed. Logical share splitting just allows each of them to know less about what the other is doing. For all Bob knew, Alice could have been speculating that A would turn out to be true, rather than actually having a proof. And it's possible that Alice had no idea when trading with Bob that Bob was trying to prove B. In short: It's nicer if the fact that A is provable is reflected in a low price for ¬A shares rather than a low price for providing the service of sticking an "∧A" onto arbitrary shares. Also, because the market mechanism only sells true or false shares, it's important to have a way to construct shares in other propositions besides proving them.)
A special case of logical share splitting is to use the law of excluded middle to mint shares on various propositions. For example, given $1, we can buy a share in ⊺ and while we're at it, we'll pick up a share in ⟂ for free. Then using equivalent exchange (and the law of excluded middle), these can be converted to shares in A∨¬A and A∧¬A for an arbitrary choice of proposition A. Then using logical share splitting (in reverse this time), these can be converted to shares in A and ¬A. Individually, these shares might have any value, but we know that the sum of their values must be $1, exactly because this trade is possible. Robin Hanson dubbed trades that convert money to shares in a proposition and its negation "splits" (to avoid confusion, we're calling this "minting") and the reverse kind of trade "joins". With the ruleset above, such operations can be decomposed into their more fundamental components: Equivalent exchange (with law of excluded middle), and logical share splitting.

Computer Assistance

In theory, any mathematician throughout history with an understanding of formal logic could have run a market of this kind. However it would be a huge amount of work to manually make and verify all trades, for relatively little benefit. A computerized market, with a well-defined API, is much more useful. We should imagine that most trades on such a market will be made by computers. Proof languages like Coq, as well as automatic theorem provers seem likely to be heavily used here. In addition, fully formal rigorous proofs are labour-intensive for mathematicians to write down, so large language models could provide a good way to convert informal proofs and arguments into the format expected by the proof system. Machine learning in general might have many interesting applications here.

Application to Ordinary Prediction Markets

While previously we've been describing a mathematical use case, there's no reason that we couldn't also include atomic shares corresponding to the outcomes of real world events. Then these could be combined logically just like questions in mathematics. For example, if A corresponds to "the next US president will be a Republican" and B corresponds to "the next US vice-president will be a Democrat", then shares could be minted for A∧B using the usual excluded-middle share-minting technique. And while both A and B shares might be trading at middling values, A∧B shares would be trading for very little, which tells us that the events corresponding to A and B are not independent.
Ordinary prediction markets deal in individual events, but there's no extra cost to allowing logical combinations of events. So long as we're able to resolve the outcome of each prediction, that tells us how to resolve all logical combinations. Here's the extra trading rule we've got to add:
In the simplest case, this rule allows converting shares in A to shares in ⊺ if event A happened, and thus redeeming them for $1.
Application: Conditional prediction markets. Say you're trading in several conditional prediction markets, conditional on an event Q. Perhaps you want to make $100 bets on predictions A given Q and B given ¬Q. The way an ordinary prediction market handles conditional predictions is to resolve to N/A when the event we're conditioning on doesn't happen. When a market resolves N/A, it means that all the traders get the money they invested back. So if I were betting on an ordinary prediction market (Manifold, say), I'd have to put up $200 in capital to make my bets. Even though only one of those two markets would ever resolve at all. The other would just give me my $100 back again.
Intuitively it seems like making those bets should only require $100 of capital, since Q and ¬Q are mutually exclusive, and whichever of the two happens to be true, I'm then only investing $100. If you've ever bet in conditional prediction markets, you may have wished that you could make investments on both sides of the conditional without the required capital needlessly doubling. Markets with logical share splitting allow this.
The way conditional prediction markets work with this ruleset is as follows: To bet on A given Q, I buy shares in A∧Q. But I don't buy them with dollars. Buying with dollars would just mean I'm investing in A∧Q itself. Instead, I buy them with shares in Q. There must be some going-rate at which other traders are willing to give me shares in A∧Q in exchange for shares in Q and it's exactly this rate that gives the conditional market price. Now to make my investment, I don't need $200. Instead I can spend $100 to mint 100 shares of Q and 100 shares of ¬Q. Then I can invest in A∧Q with my Q shares and in B∧¬Q with my ¬Q shares. Note that if I just hold on to my shares for ¬Q rather than investing them, then we're back at Robin Hanson's original formulation of what it means to invest in a conditional: I get my investment back if Q doesn't happen.

Subsidizing the Market

In our example above, Alice and Bob were driven to prove B because its shares had a price of only $0.6, even though it was provable. It's well known that in order to run a prediction market, it must be subsidized, where prices in a proposition and its negation sum to slightly less than $1. Otherwise, trading in the market is a zero-sum game and participants would on average have no reason to play. Therefore, the people who want to know the answer for a particular question have a reason to subsidize the market for that question.
But wait a second: Suppose that we're subsidizing the market in A so that prices for A and ¬A sum to $0.99, say, instead of $1. This permits an arbitrage: Buy shares in A and ¬A from the subsidizers for $0.99, and then do a join to get $1 out, for a profit of $0.01. This is not what we wanted, we're basically just giving away pennies for free. As subsidizers, we're fine with losing money on the deal, but we want that money to end up stuck in shares that can only be redeemed by actually proving the proposition we're interested in. If traders can make a profit right away by just cancelling out all their shares with each other, that doesn't accomplish our goal.
We might be able to get around this by talking about proofs instead of propositions directly. In other words, we could request a proof or disproof of the Riemann hypothesis by separately subsidizing shares in ☐R and ☐¬R. These are not the negations of each other, so they can't be cancelled out. The market mechanism just auctions off a bunch of ☐R shares without counter-balancing ¬☐R shares. And these auctioned shares can then only be redeemed by proving the Riemann hypothesis. Or, at least by proving that the Riemann hypothesis has a proof. There's a chance that someone might find a non-constructive proof of ☐R, though it's possible for human observers outside the system to decide they're willing to extend their axioms so that such non-constructive proofs of ☐R would themselves count as proofs of R.

Appendix: Completeness

It turns out that these laws of trading are complete in the sense that they allow the conversion of any set of shares into any other set of shares of equivalent value. Where equivalent value means that the two sets of shares can be redeemed for the same amount of money, regardless of how all the underlying propositions resolved. (The setup here is that we have some underlying propositions, A, B, C, ... each of which can be either true or false. These could be prediction market predictions, or (though the math here would be kind of poorly-defined) they could be propositions that do not yet have proofs or disproofs.)
For ease of understanding, I'll give a "proof" by example. Suppose that X is some expression of the propositions A, B, C. Then we can express it in disjunctive normal form. Say it comes out as: X = (A∧B∧C)∨(A∧B∧¬C)∨(¬A∧¬B∧C). For short, we'll define A∧B∧C = P; A∧B∧¬C = Q; ¬A∧¬B∧C = R so that X = P∨Q∨R. We'll call the expressions P, Q, R "one-hot" expressions, since they're each true for exactly one of the possible outcomes. We can convert a share in X into shares in the underlying one-hot expressions as follows:
P∨Q∨R start from X
P∨Q∨R, ⟂ buying false is free
P∨Q∨R, P∧(Q∨R) equivalent exchange (different one-hot expressions are contradictory)
P, Q∨R logical share splitting
We can repeat the process until we have shares in each separate one-hot expression.
P, Q∨R, ⟂ buying false is free
P, Q∨R, Q∧R equivalent exchange
P, Q, R logical share splitting
We can convert a share in any logical expression into its component one-hot expressions like this. By applying the conversion to all shares in the set, we can convert any set of shares into an equivalent set of one-hot shares. Because all laws of trading are reversible, this means we can convert any set of shares into any equivalent set by first converting to the equivalent set of one-hot shares, and then converting to the desired share set.

Appendix: See Also

This is all closely tied to the theorem in probability that P(A) + P(B) = P(A∧B) + P(A∨B). The concept of a valuation also seems to be very related.