The usual conception of a heat engine looks like this:

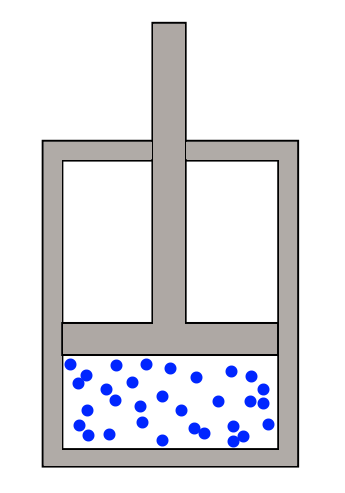
Some gas is contained in an enclosure. The gas is first heated up, and expands, pushing on the piston. This gives us some energy, which can be stored in the spinning of a flywheel, for example. Then the gas is cooled down, and we can push the piston back into the cylinder while using using a lesser quantity of energy. Since the push outwards yielded more energy than the push inwards consumed, we can generate a bunch of useful energy just by repeating the whole process many many times.

The whole thing works because when the gas is hot, it has a larger pressure than when it is cold, so by expanding when hot and compressing when cold, we can extract net useful energy. This can be seen from the ideal gas law which relates temperature, pressure, and volume.

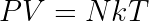
here, N is the number of particles in the gas, which stays the same so long as no particles can leak in or out of the cylinder, and k is Boltzmann's constant, which is a fundamental physical constant.

The "best" way we have of running the cylinder engine is called the Carnot cycle. Imagine we have a large bath of hot water, and another large bath of cold water. We can assume that these are sufficiently large that adding or removing some heat won't change the temperature very much: water can store a lot of thermal energy. Heat flows from hotter objects to colder ones. It does this because two objects of medium temperature have a larger entropy than one hot object and one cold object. Entropy tends to increase, and so the objects will exchange heat in an attempt to bring about the situation where they both have the same temperature. But this has implications for us when designing a heat engine.

Ideally, we want to create as little new entropy as possible. The heat from the hot bath inevitably carries with it some entropy, and so we have to pay some energy cost to get rid of that entropy into the cold bath. But we certainly shouldn't be making any new entropy for ourselves to deal with. Therefore, when we're pulling energy from the hot bath, the temperature of our gas in the cylinder should be the same as the temperature of the hot bath. It needs to be just the tiniest fraction less, in order for heat to flow, but we want the difference to be as small as possible, so that no entropy is created. Similarly, when we're dumping energy into the cold bath, we want the gas to be just the tiniest bit hotter than the cold bath. So during the phases of the Carnot cycle when the gas exchanges energy with the baths, we want the temperature of the gas in the cylinder to be constant and the same as that of the bath.

Then the remaining question is how we shift the gas from hot to cold and from cold to hot. During these phases of the Carnot cycle, no energy is exchanged between the gas and its environment: Exchanging heat at an intermediate temperature would create new entropy, and therefore make our heat engine less efficient than it otherwise would be. We can imagine that the cylinder is surrounded by insulating foam, as opposed to being dipped in either the hot bath or the cold bath. Therefore, we're forced to heat the gas by pushing on the piston to compress it, and to cool the gas by allowing the gas to expand and push the piston outwards. We call this "adiabatic" expansion and compression, when the gas is being heated and cooled without it exchanging any heat with its surroundings. We want to heat and cool the gas adiabatically, and produce no entropy in the process. This requires that the piston doesn't move too quickly: We can imagine that if we shake the piston back and forth very quickly, it will produce sound waves in the gas that echo through the cylinder and dissipate into heat, increasing entropy. Or if we pull the piston out extremely suddenly, then it will create a vacuum, which the gas will rush to fill in a very messy way, increasing the entropy. But so long as we move the piston slowly enough, the entropy stays the same, while the temperature and volume go up and down as we slide the piston back and forth.

So overall, the carnot cycle looks like the following, with A⇒B representing the isothermal heating phase, B⇒C representing adiabatic expansion, C⇒D representing isothermal cooling, and D⇒A adiabatic compression.

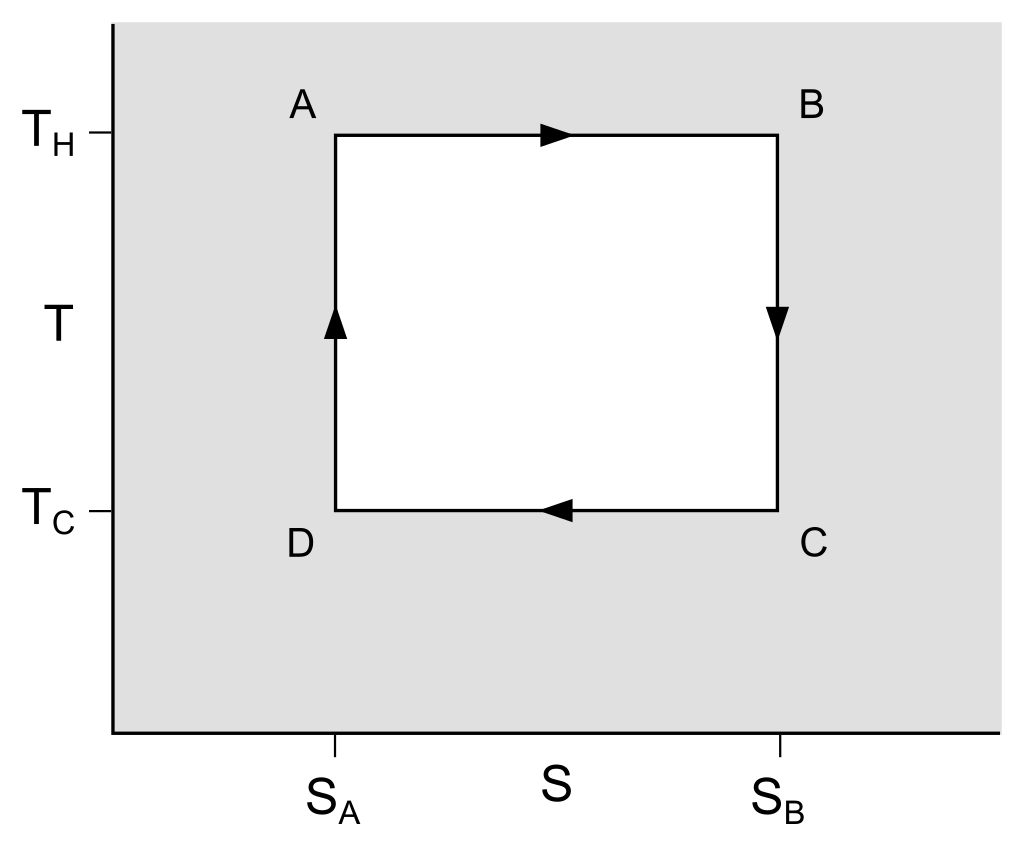
Why is an engine using the Carnot cycle an impractical heat engine? For the reason that it's not powerful enough. Though the engine is very efficient, when the difference in temperature between two objects is infinitesimal, it takes an enormously long time for heat to flow between them. There's no fundamental thermodynamic principle here limiting the rate of heat flow, it just happens that most materials can't conduct heat very quickly. Even if the body of the cylinder were made from a material that conducts heat instantly, the heat would take some amount of time to flow through the gas, though this is fast enough that Stirling engines work by shuffling gas between a hot cylinder and a cold cylinder and allowing it to heat up and cool down there. This, plus the use of a non-Carnot cycle that wastes some free energy in exchange for power allows the Stirling engine to be a practical engine.

The exceedingly practical and powerful internal combustion engine deals with the problem of heating and cooling in a different way. Rather than cooling the gas down, it pushes the hot gas out of the cylinder, and pulls in new cold gas from outside. (Conveniently, this cold gas also contains the oxygen necessary to actually burn the fuel.) And its method of heating the gas up is to mix some fuel into it, and then detonate it. Done properly, the fuel is evenly mixed throughout the gas, and so the detonation heats up every part of gas simultaneously, ensuring that heat transfer is not a problem.