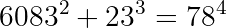
Diophantine Equation: a²+p³=b⁴

2022 Apr 20

The nice thing about math videos on youtube is that sometimes the statement for the problem to be solved in the video is simple enough to fit in the thumbnail. In that case, you can just read the problem off the thumbnail and try to solve it yourself without watching the video. One such problem (from a Michael Penn video I think) is to find the smallest prime p that solves the following equation (where the variables must all take on integer values):

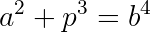
The way this will work, is there will be a couple of places where we analyse by cases, and always there will be only one path that provides solutions, and any other path will be a dead end. We'll call such cases where there are no solutions "dead cases", and give proofs that they are empty of solutions. Cases that harbor solutions will correspondingly be called "living cases". The starting point will be to rearrange and factor:

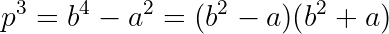
Without loss of generality, we can take a to be positive, which implies that both factors must be positive, so we have 2 cases:

Dead Case:

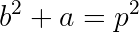
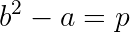
We can then reason as follows:

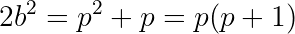
If p is 2, then 2b²=6, and b cannot be an integer.

If p is greater than 2, then 2b² contains exactly one factor of p, so b cannot be an integer.

Living Case:

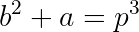
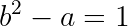
We can then reason as follows:

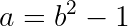
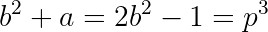
It will be useful to eliminate the possiblity that p=2 in all subsequent reasoning, so that we can assume that p is an odd prime. This can be seen by plugging 8 for p³ above, and observing that there are no solutions.

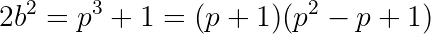
Note that only the p+1 factor can be even. Also, the overall product must be twice a square. So we can find positive numbers x, y, z, with y being squarefree and both y and z being odd such that:

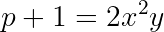
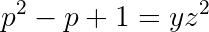
This implies:

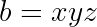
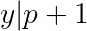
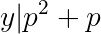
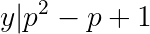
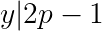
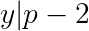
Since y divides both p+1 and p-2, y must be equal to 1 or 3.

Second Dead Case:

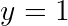
We can then reason as follows:

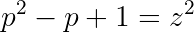
Note that since p is an odd prime:

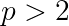
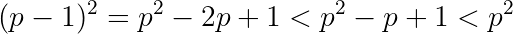
Since z² would have to be between adjacent squares, there are no solutions in this case.

Second Living Case:

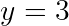
We can then reason as follows:

$z^2=1 \mod 4$

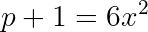
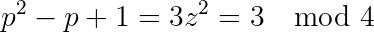
$p^2-p+1 = 3z^2 = 3 \mod 4$

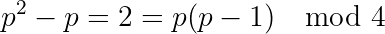
$p^2-p = 2 = p(p-1) \mod 4$

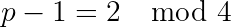
$p-1 = 2 \mod 4$

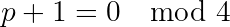
$p+1 = 0 \mod 4$

Therefore x² is even which means x is even. Let w = x/2. Then:

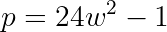
Now we can start plugging in w=1,2,3,4... and see how soon we get a prime. The resulting sequence is:

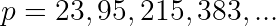
It turns out that the very first element, p=23, is prime. That's our answer. Now constructing a solution to the equation is just a matter of subbing back for b and a:

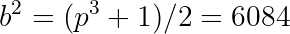
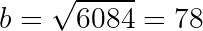
$b = \sqrt{6084} = 78$

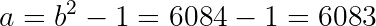
Therefore our solution to this equation is: