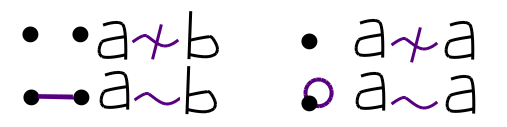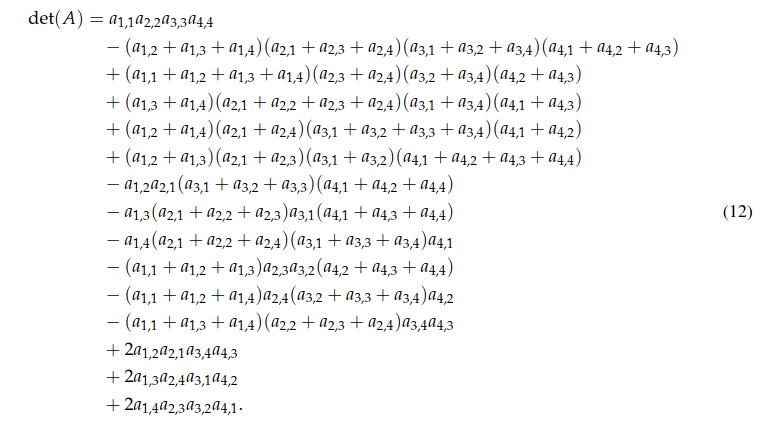Houston's Determinant Identity Explained
2023 Mar 23
You'd think we'd already know just about everything there is to know about the determinant. And yet: Robin Houston has recently discovered
an interesting new formula for the determinant! It's always exciting when new mathematical progress is made on something so fundamental. So what's interesting about the formula? The determinant in
n dimensions is a degree-
n polynomial, and the conventional formula for the determinant is a sum of
n! terms. Houston's identity instead consists of a sum of
B terms where
B is the
nth
Bell number. (Bell numbers grow very quickly, a little faster than exponentially, but still slower than the factorial.)
The Formula
So let's dive into the formula. It looks like this for a n×n matrix:
Above,
ℙℙ denotes the set of partial partitions of the numbers from
1 to
n (we denote this set as
ℕ). A partition is a set of subsets of
ℕ where each number
a∈ℕ is contained in exactly one of the subsets. A partial partition is similar, but more permissive: Instead of being contained in exactly one subset,
a must be contained in at most one subset. So we have the option of leaving numbers out, as well as assigning them to a particular subset.
A given partial partition
P defines a relation
∼ on
ℕ, which works like this:
a ∼ b ⇔ ∃S∈P; a∈S ∧ b∈S So this relation is a bit like an equivalence relation, except that it's possible for a number
a to be contained in none of the sets in
P so that
a≁a.
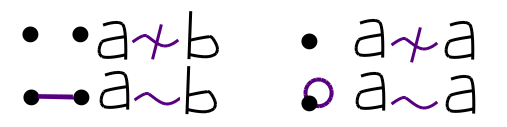
Finally, the sign of a partial partition is defined by analogy with the sign of a partition, which is defined by analogy with the sign of a permutation. The sign of a permutation can be decomposed into a product of the signs of the cycles making up the permutation. The sign of a cycle
S only depends on the size of the cycle: It's
(-1). Therefore, we can treat a partition as a permutation where each part of the partition corresponds to a cycle. We can't know the ordering of the elements in the cycle, since the original partition has no ordering, but this doesn't affect the sign, so it doesn't matter. So we have the following formula for the sign of a partition:
This is also the formula for the sign of a partial partition, the only difference is that we now allow elements to be left out of P entirely. What happens when we leave an element a out? If the element was originally contained in a singleton part S = {a} then the part contributed a factor of 1 to the sign, so the sign is unchanged. So having elements left out of the partition is pretty much the same as those elements being singletons (or 1-cycles or fixed points) as far the the sign function is concerned.
Simple Cases
n = 1
The simplest of simple cases! There are two partial partitions in
ℙℙ(1):
{} and
{{1}}. In the case where
P = {{1}} we have
1∼1 and then the sum
a is empty. So there is no contribution from
P = {{1}}. In the case where
P = {} we have
1≁1 and then the sum
a + a amounts to just
a. So overall, the formula ends up being:
det A = sign({}) |{}|! (a) = (1)(0!)(a) = a
No Singletons Rule
Whenever the partial partition P contains any singletons, the corresponding term in the sum is zero. So effectively, we can ignore any partial partitions that contain singletons. The example partition given above contains two singletons, so its contribution would be 0. The following partial partition could still be included, though:
Why is the contribution 0 when there are singletons? Suppose we have a partial partition P that contains a singleton {k}. Then consider the factor corresponding to i = k in the following product:
Since
{k} is a singleton, we have
k ∼ k and so the factor is:
However, exactly because {k} is a singleton, nothing is related to k besides k itself! Therefore the sum is empty, meaning it totals to zero. And if even a single factor in a product is 0, the entire product is 0. Thus, we can ignore any partial partition that has singletons, since they won't contribute anything to the formula.
n = 2
We can now exploit the no-singletons rule to figure out the determinant formula for 2 dimensions. The partial partitions of 2 elements with no singletons are: {} and {{1,2}}. For P = {} we get:
sign({}) (0!) (a)(a) = aa
For P = {{1,2}} we get:
sign({{1,2}}) (1!) (a)(a) = -aa
This gives the expected determinant formula:
n = 3
The partial partitions of 3 elements with no singletons are: {}, {{1,2}}, {{2,3}}, {{3,1}}, and {{1,2,3}}. The corresponding terms in Houston's identity are:
sign({}) (0!) (a)(a)(a) = aaa
sign({{1,2}}) (1!) (a)(a)(a + a + a) = -aa(a + a + a)
sign({{2,3}}) (1!) (a)(a)(a + a + a) = -aa(a + a + a)
sign({{3,1}}) (1!) (a)(a)(a + a + a) = -aa(a + a + a)
sign({{1,2,3}}) (1!) (a + a)(a + a)(a + a) = (a + a)(a + a)(a + a)
This gives the following determinant formula:
det A = aaa − aa(a + a + a) − aa(a + a + a) − aa(a + a + a) + (a + a)(a + a)(a + a)
This formula has only 5 terms, whereas the conventional determinant would have 6. It turns out this formula for the determinant was already known. But the advantage of Houston's identity is that we can keep going to 4 and beyond to generate new determinant formulas.
n = 4
Here's a brief excerpt from the paper, showing the new 4 dimensional determinant formula:
When n = 4, Theorem 1 gives the following 15-term formula for the determinant (surpassing the prior state of the art formula, which has 20 terms):
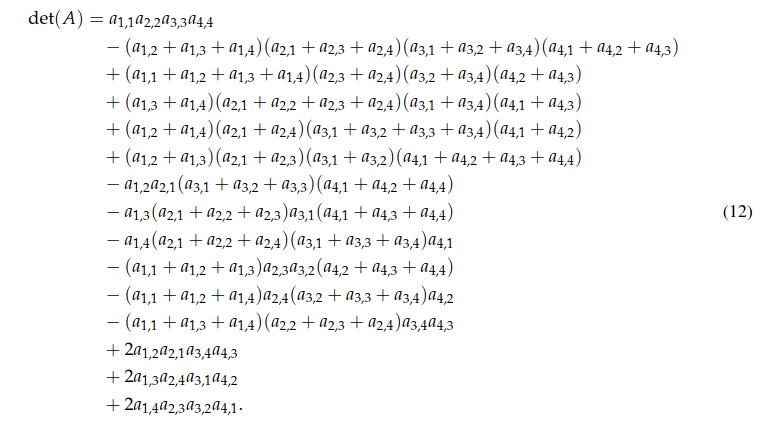
Proof
I'll now try to explain the proof that the authors give in their paper, specifically the combinatorial proof.
How do we know that Houston's identity actually computes the determinant? We should first recall the canonical formula for the determinant:
As mentioned above, the determinant considered as a function of matrix entries is a degree-n polynomial. Furthermore, the determinant is homogenous, meaning that each term in the polynomial has the same degree. Finally, if we zoom in and look in on a particular term, we'll see that it contains exactly one element from each row of the matrix. (This is easy to see just by noting that the product is over all i up to n.) By inspecting Houston's identity, we can see that the same is true of it. So we just need to verify that the coefficients for each term of this type are equal. If the following is true, then we have succeeded in proving Houston's identity:
Where
f: ℕ → ℕ is a function and the
C are the coefficients of the polynomial produced by Houston's identity. The following formula defines the
C:
In other words, if we expand Houston's identity, the coefficient
C corresponding to a function
f should be zero if
f isn't a permutation, and should be equal to the sign of that permutation otherwise. Note that the term corresponding to
f takes the matrix element
a from row
i. Asking that
f be a permutation is equivalent to asking that the corresponding term has exactly one matrix element from each column, just like it has exactly one matrix element from each row.
So now we have our goal: We need to expand the formula on the left to get the coefficients and then make sure that they're the coefficients we're expecting.
The first question to ask is: Which partial partitions actually contribute to a given coefficient? The answer is the following:
Consider the factor corresponding to
i. Let
P be any given partial partition. First suppose that
i∼i. Then
j only appears in the factor if
j∼i ∧ i≠j. Thus, in order for the term to contribute to
C it must be true that
i∼f(i) ∧ i≠f(i). On the other hand, suppose that
i≁i. Then
j only appears in the factor if
j=i ∨ j∼j. Thus in order for the term to contribute to
C it must be true that
i=f(i) ∨ f(i)∼f(i). We can combine these two cases with a logical OR, and apply this formula to all factors in the product to determine which partial partitions contribute to
C:
∀i∈ℕ; (i∼i ∧ i∼f(i) ∧ i≠f(i)) ∨ (i≁i ∧ (i=f(i) ∨ f(i)∼f(i)))
∀i∈ℕ; (i∼i ∧ i∼f(i) ∧ i≠f(i)) ∨ (i≁i ∧ i=f(i)) ∨ (i≁i ∧ f(i)∼f(i))
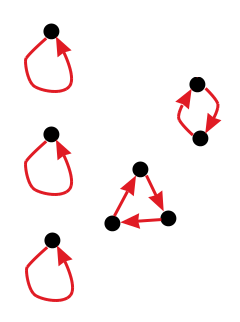
We can see that this second expression (equivalent to the first expression) breaks into 3 cases:
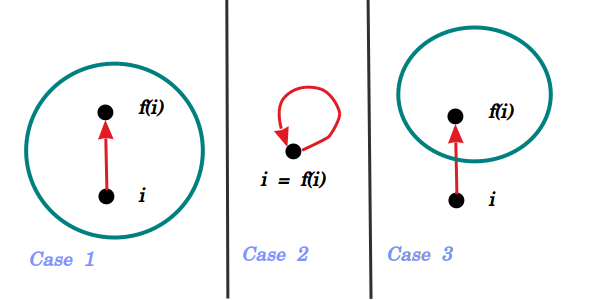
Case 1:
i∼i ∧ i∼f(i) ∧ i≠f(i)The following diagram shows them visually:
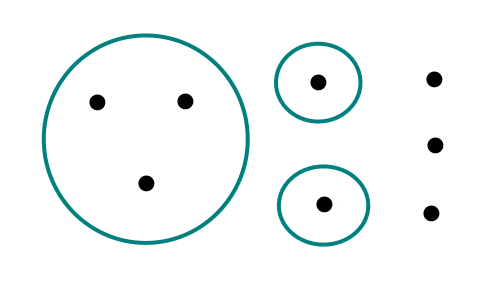
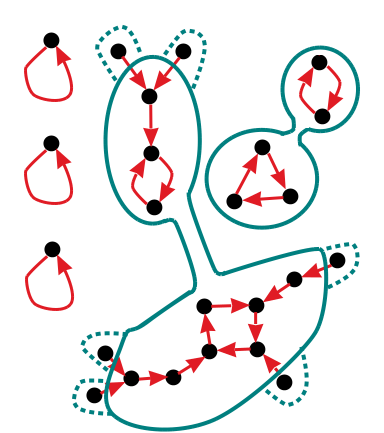
Now what kinds of things is it possible for functions to look like? Since each number is mapped by the function to exactly one other number, if we apply the function repeatedly, we should end up in a cycle. This includes fixed points, which are a special case of a cycle of length 1. But before reaching a cycle, there might be a sequence of other numbers, which must be arranged in a tree. So overall, a typical function might look like this:
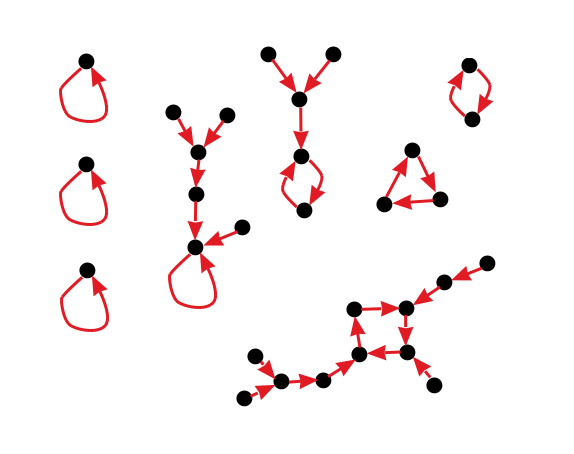
Now we can eliminate one class of functions right away, because they don't have any contributing partial partitions. These are the functions that have fixed points with trees growing off of them. By case 2 above, fixed points must not be included in any parts. But by case 1 or case 3, anything mapped to by another point must be inside of a part. So there can't exist any partial partitions that satisfy the criteria to contribute to the term for f.
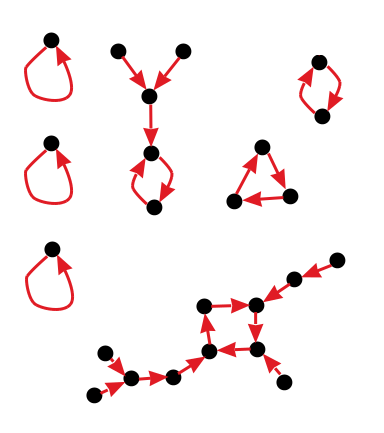
So the remaining functions would consist of isolated fixed points, along with cycles of length at least 2. These cycles can still have trees growing off them. So the remaining functions
f that have a hope of having non-zero
C typically look something like this:
For the remaining functions, what do the relevant partial partitions look like? Consider a cycle of length at least 2. By cases 1 and 3, all the numbers in the cycle must be enclosed in some part, along with all the numbers in the trees growing off that part, except for the leaves. We have a choice for each leaf: We can include it in the same part as the cycle it's growing from, or we can leave it out of all parts. There are
2 possibilities for this. Note that while each cycle must be contained in the same part, it's possible for one part to contain multiple cycles. So the number of possibilities for how the cycles are distributed amongst the parts is
B. (Note that #cycles only counts cycles of length at least 2, we're leaving out the fixed points here.)
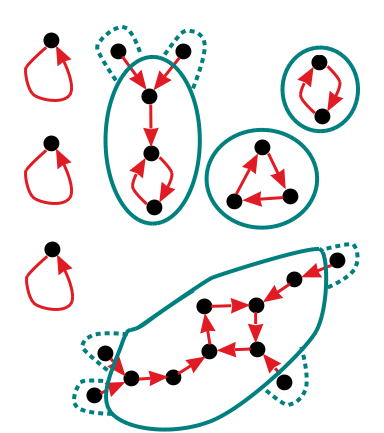
Now consider one particular way, amongst the
B ways to divide the cycles amongst the parts. We then have
2 remaining options for our choice of partial partition. The factor
|P|! is fixed since we've fixed the number of parts. Consider what happens when we move a leaf from being left out all parts to being contained in a part. This yields a factor of
-1 from
sign(P). So if we now consider the sum over all possible combinations of including and not including each leaf, we get a factor of
(1-1) = 0 This is 0 unless we have no leaves, in which case it's 1. So we've shown something that's actually very interesting: If we don't want
C to be zero, then we need
f not to have any leaves. And all trees have leaves, so we actually require that
f not have any trees. In other words,
f must be a permutation.
So what remains is to figure out, for any given permutation
f what
sign(P) |P|! sums to. To give ourselves some notation to work with, we'll write the set of partial partitions that contribute to
C as
ℙℙ(n). Then we have:
First, to make things easier a bit later, we'll note that we can rewrite the sign of a partial partition in terms the sign of f. As a base case, note that if we let the parts of P be the cycles of f of length at least 2, then the sign of that partial partition is sign(f). Now suppose that some other partial partition, the one whose sign we are really interested in, has m parts. We can note that merging 2 parts always flips the sign, and after a little bit of thought, we can derive the formula:
sign(P) = (-1)(-1)sign(f)
Now, we can break down the partial partitions in terms of the number of parts they have,
m = |P|. We'll use the sign formula in terms of
m, and the fact that the number of partitions with
m parts is
{}:
C = {} (-1)(-1)sign(f) m!
C = sign(f) (-1) {} (-1) m!
Now we use a nice property of Stirling numbers that was proved
here. It looks like this:
If we pick x = -1, then we have:
= (-1)(-2)(-3)...(2-m)(1-m)m = (-1) m!
So by the above Stirling number identity:
But this is exactly what we wanted to show!
C is 0 unless
f is a permutation, in which case it's
sign(f). So this concludes the combinatorial proof of Houston's identity.
Further Reading
See the following to read about this firsthand, and learn about the geometric interpretation of this formula based on tilings.
Houston originally posted about the identity
on Twitter.